Eingabewerte und Ergebniswerte
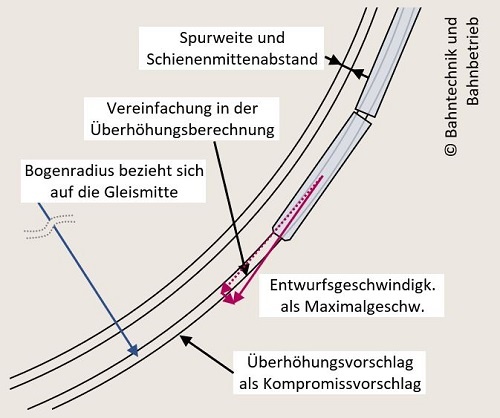
1. Die Spurweite hat als Standardwert 1435 Millimeter angegeben, aber es sind auch andere Spurweiten als Eingabewert möglich. Mit der Spurweite wird der Schienenmittenabstand berechnet und geht als Wert in die weitere Berechnungslogik mit ein.
2. Die angedachte Entwurfsgeschwindigkeit ist eines von mehreren Eingabeparametern zur Ermittlung der Überhöhung. Sie trägt als Einheit Kilometer pro Stunde und ist schließlich die maximale Geschwindigkeit, mit welcher die Züge den Trassierungsbogen befahren dürfen.
3. Der angedachte Entwurfsradius ist der Trassierungsradius des Bogens, und zwar in der Einheit Meter angegeben.
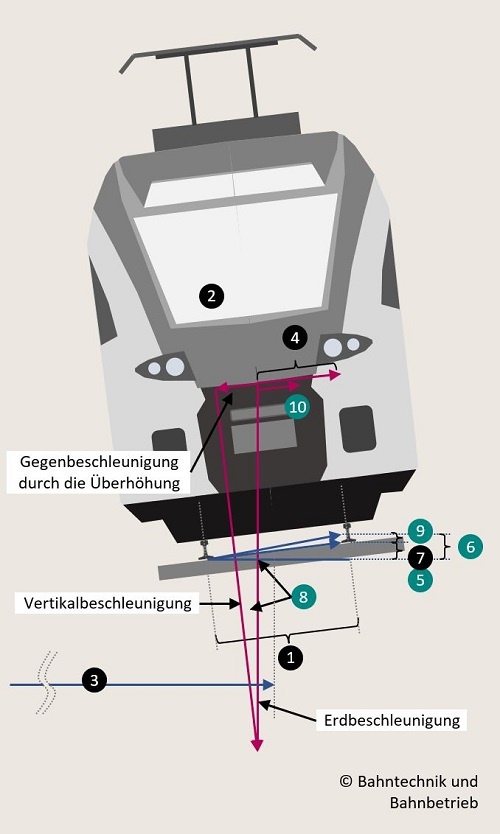
4. Als resultierende Zentrifugalbeschleunigung wird die Fliehkraftbeschleunigung verstanden, die ein Zug bei dem gegebenen Entwurfsradius und der gegebenen Entwurfsgeschwindigkeit erfahren würde, wenn er diese Geschwindigkeit ausreizen würde. Bei dieser resultierenden Zentrifugalbeschleunigung ist noch keine Überhöhung unterstellt. Als Einheit ist der resultierende Wert in Meter pro Sekunde in Quadrat beschrieben.
5. Aus der resultierenden Zentrifugalbeschleunigung und einem Standardwert für eine akzeptable Seitenbeschleunigung für Fahrgäste resultiert dann ein empfohlener Vorschlagswert für eine Regelüberhöhung. Diese Regelüberhöhung hat die Einheit Millimeter.
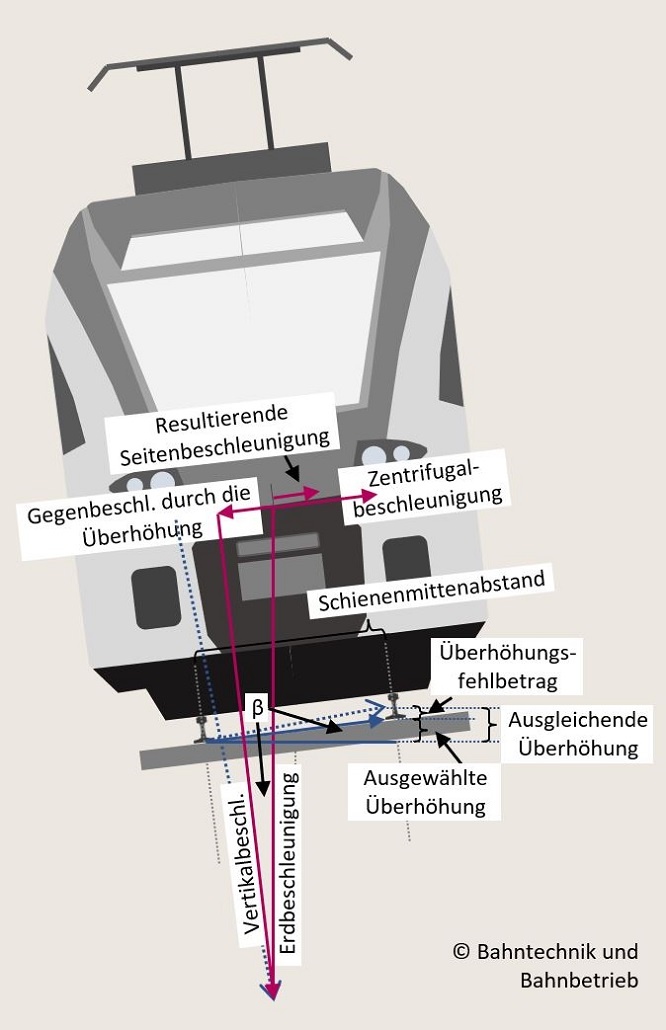
6. Bei der ausgleichenden Überhöhung ist die Außenschiene um den Millimeterwert so erhöht, dass die Zentrifugalbeschleunigung und somit die Seitenbeschleunigung für die Fahrgäste bei den vorgenannten Parametern gleich null beträgt.
7. In diesem Eingabefeld ist die bevorzugte Überhöhung nach den vorgenannten Informationen wie die Regelüberhöhung oder der resultierenden Überhöhung einzutragen.
8. Anhand der ausgewählten Überhöhung resultiert ein entsprechender Fahrbahnneigungswinkel, welcher in Winkelgrad ausgewiesen wird.
9. Der resultierende Überhöhungsfehlbetrag ist der Betrag an Überhöhung in Millimetern, der noch für eine zentrifugalkraftfreie Befahrung des Bogens fehlt. Zugleich ist er die Differenz aus (6) und (7).
10. Die resultierende Querbeschleunigung ist die Seitenbeschleunigung, die auf die Fahrgäste bei gegebener Entwurfsgeschwindigkeit, Entwurfsradius und der gewählten Überhöhung wirkt.
Physikalische Annahmen
Bei der Berechnung der Überhöhung und der resultierenden Seitenbeschleunigung sind folgende physikalischen Annahmen und Vereinfachungen unterstellt:
1. Die Entwurfsgeschwindigkeit wird auch bei der Zugüberfahrt eingehalten. Hat der Zug eine höhere Geschwindigkeit, so steigt dann auch die resultierende Seitenbeschleunigung, ist sie niedriger, so sinkt die resultierende Seitenbeschleunigung. Statt der Entwurfsgeschwindigkeit kann auch die tatsächlich gefahrene Geschwindigkeit eingegeben werden.
2. Der angedachte Entwurfsradius beim Gleisbogen bezieht sich auf die Gleismittenachse.
3. Der Überhöhungsvorschlag ist ein in Verkehrsunternehmen ausgearbeiteter Kompromiss aus Wirtschaftlichkeit und Trassierungsfreiheit. Als relevante vertretbare Seitenbeschleunigung für Fahrgäste wurde der Wert so erwählt, dass er ungefähr 55 % der ausgleichenden Überhöhung entspricht.
4. Die resultierenden Überhöhungen als auch der resultierende Fahrbahnneigungswinkel beziehen sich stets auf Gleise mit einem Schienenmittenabstand, der idealisiert über die Spurweite berechnet wird. Bei einer Spurweite von 1435 mm beträgt der Schienenmittenabstand zum Beispiel 1500 mm.
5. Alle Überhöhungsberechnungen gelten nur für geringe Fahrbahnneigungswinkelunter 10 Grad. Grund dafür ist, dass in der Berechnung eine Vereinfachung vorgenommen wurde. (siehe auch Formel und Herleitung, Schritt (3))
Formeln und Herleitung
Im ersten Schritt gilt die allgemeine physikalische Formel für die Zentrifugalbeschleunigung. Sie ist abhängig von der gefahrenen Geschwindigkeit und vom Radius des Befahrungsbogens. In einem weiteren parallelen Schritt wird ein Kräftegleichgewicht angenommen. Eine wirkende Hangabtriebskraft wirkt der Zentrifugalkraft entgegen. In (2) ist also erster Term gleich zweiter Term, man kann die Terme sogar nur auf die Beschleunigung reduzieren, da die Massen konstant sind. Sie kürzen sich also raus. In (3) nimmt man an, dass der Cosinus für kleine Winkel Beta ungefähr den Wert eins annimmt.
Anschließend werden die allgemeine Zentrifugalbeschleunigung und die Annahme in (3) in der Formel (2) berücksichtigt.
In Schritt (4) gibt es noch eine weitere parallele Erkenntnis. Der Term Sinus Beta ist über die Winkelkongruenz ebenso eruierbar. Sinus Beta ist die Ankathete durch die Hypothenuse, also in unserem Fall auch die ausgleichende Überhöhung geteilt durch den Schienenmittenabstand. Diese Erkenntnis ebenso in (2) eingesetzt ergibt (6). Alles aufgelöst nach dem ausgleichenden Überhöhungswert aufgelöst, ergibt dann die allgemeine Formel für die Überhöhung.
Da aber die ausgleichende Überhöhung meistens nicht wirtschaftlich vertretbar ist, gibt es eine Regelüberhöhung, die als Empfehlung gelten kann (8).
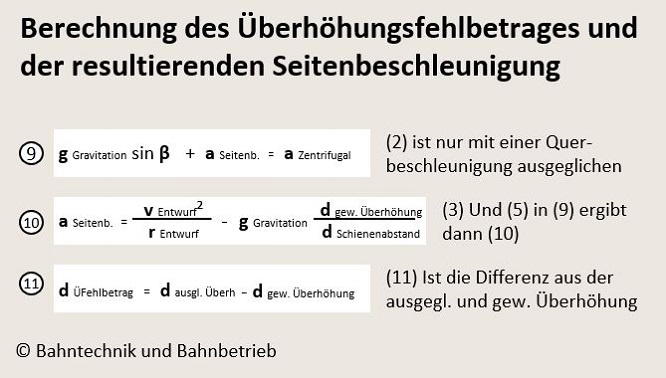
Wenn die ausgleichende Überhöhung bautechnisch nicht ausgeschöpft wird, dann muss die Formel (2) noch um eine restliche Seitenbeschleunigung ergänzt werden. Diese entsteht und wirkt auf den Zug und die Fahrgäste. Die entsprechende abgewandelte Formel aus (2) lautet dann gemäß der Formel (9).
Diese Formel mit den zuvor genannten Erkenntnissen angereichert ergibt dann die Formel (10).
Über alle resultierenden Überhöhungen lässt sich dann der Überhöhungsfehlbetrag errechnen. Der Überhöhungsfehlbetrag plus die ausgewählte Überhöhung ergeben nämlich die ausgleichende Überhöhung.














Hallo Alexander, Danke für dein tolles Feedback. Noch kurz zu deiner fachlichen Ausführung: so wie die Grafiken sind, ist es meines Erachtens richtig. Und auch laut Fachbüchern ist es immer so dargestellt. Wäre es nach Deiner Beschreibung, dann wäre die Vertikalbeschleunigung in einer anderen Diagonalen, und sie wäre dann größer als die Erdbeschleunigung. Dies ist aber fachlich nicht so. Die Vertikalbeschleunigung wird durch zunehmende Zentrifugalbeschleunigung geringer, dies spürt man auch, wenn man Karusell fährt…
Danke dennoch für Deine Beteiligung.
Beste Grüße
Johannes