Eingabewerte und Ergebniswerte
1. Unter dem Dropdownfeld „Triebfahrzeugtype“ kann der Bediener ein Triebfahrzeug auswählen, für welchen viele verschiedene physikalische Parameter hinterlegt sind. Unter 1b kann der Bediener die Anzahl der im Zugverband gekoppelten Triebfahrzeuge eingeben. Diese und nachfolgende Eingabedaten werden beim Zugkonfigurator genauer erläutert.
2. Falls unter 1a eine Lokomotive ausgewählt ist, dann erscheint das Dropdownfeld „Wagentype“. Hier kann der Bediener einen konkreten Wagentyp auswählen. Unter 2b gibt der Anwender die Anzahl der Wagen ein.
3. Über den Auslastungsgrad wählt der Bediener aus, wie sehr sein ausgewählter Zugverband mit Fahrgästen bzw. mit Gütern ausgelastet ist.
4. Die mittlere Steigung oder Neigung wird gemäß der bahntechnischen Planung in Promille angegeben. Hier sind Werte zwischen -40 Promille (Neigung) bis +40 Promille (Steigung) erlaubt.
5. Durch die Fahrzeug- und Wagenauswahl berechnet der Beschleunigungsrechner die resultierende Zuglänge als Kontrollwert. Dieser ist angegeben in Metern.
6. Über die Fahrzeug- und Wagenauswahl lässt sich auch das resultierende Zuggewicht, angegeben in Tonnen, als Kontrollgröße berechnen.
7. Die verbaute Motorleistung durch die Triebfahrzeugauswahl kann der Bediener diesem Ergebnisfeld entnehmen. Die Einheit ist Kilowatt.
8. Die resultierende Haftreibmasse ist die Masse, die sich auf eine translatorische Bewegung umsetzen lässt. Sie ist die Masse, angegeben in Tonnen, die auf alle Antriebsachsen wirkt.
9. Durch den Ausreizungsgrad der Zugkraft lässt sich festlegen, inwiefern das Fahrpersonal die verfügbare Zugkraft über den Fahr- und Bremshebel ausnutzt. Dieser Wert ist in Prozent einzugeben.
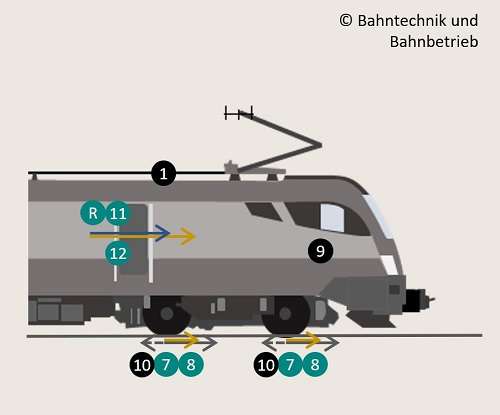
10. Der Schienenzustand bestimmt den Beschleunigungsvorgang insofern, dass bei entsprechend schlechten Wetterverhältnissen die Haftreibung zwischen Rad und Schiene nachlässt. Dadurch kann sich der Beschleunigungswert erheblich verschlechtern.
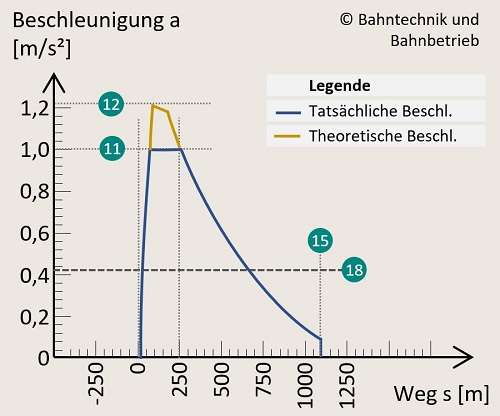
11. Der Beschleunigungswert besteht aus einer durch die Haftreibung und durch die Motorleistung bestimmter Beschleunigungswert. Dieser wird aber fahrzeugtechnisch gedrosselt, um einen gewissen Fahrgastkomfort zu erfüllen bzw. eine Überbeanspruchung von Bauteilen zu vermeiden. Diese tatsächliche Beschleunigung bestimmt den weiteren Rechenverlauf und hat die Einheit Meter pro Sekunde zum Quadrat.
12. Die theoretische Beschleunigung ist der vorgenannte Wert ohne dieser fahrzeugtechnisch projektierten Regulierung.
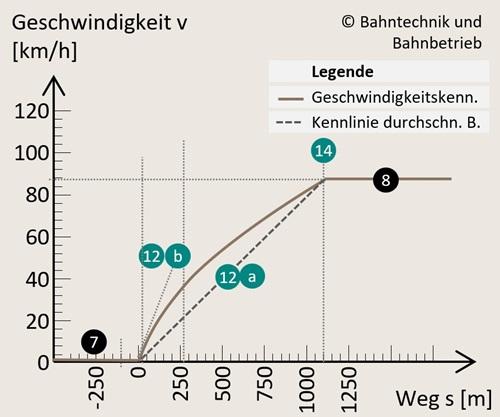
13. Die Startgeschwindigkeit, angegeben in Kilometer pro Stunde, ist die Geschwindigkeit mit welcher der Zug vor seinem Beschleunigungsvorgang startet.
14. Die Zielgeschwindigkeit ist die Geschwindigkeit, welche der Zug nach seinem Beschleunigungsvorgang erreichen soll.
15. Der resultierende Beschleunigungsweg ist der gesuchte Weg in Metern, den der Zug für seinen Beschleunigungsvorgang zurücklegt.
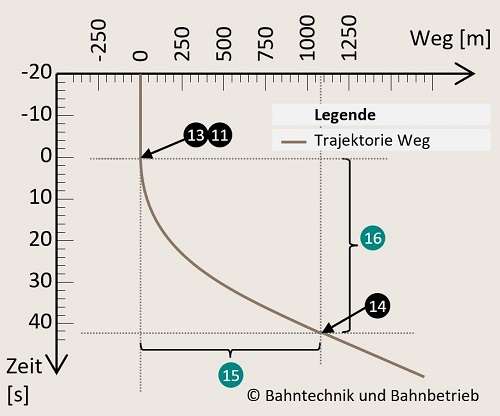
16. Die Beschleunigungszeit ist die gesuchte Zeit in Sekunden, die der Zug für seinen Beschleunigungsvorgang benötigt.
Physikalische Annahmen
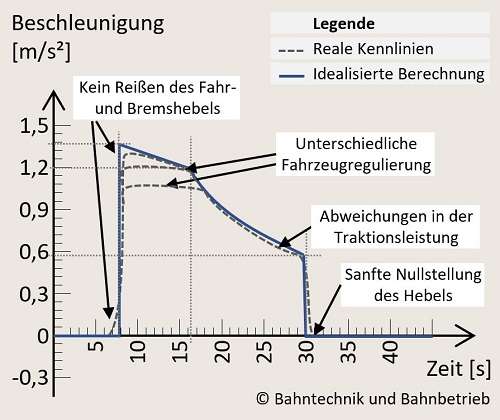
Die Berechnung der Beschleunigung kann nur mit vielen Annahmen durchgeführt werden, weil an diesem fahrdynamischen Vorgang viele physikalischen Einflüsse vorherrschen. Es sind folgende physikalischen Annahmen und Vereinfachungen unterstellt:
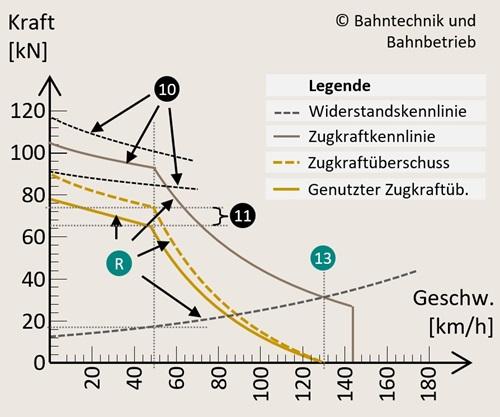
1. Die Kraftschlussgrenze ist die maximale mögliche Zugkraft, die gerade noch ein Durchdrehen der Räder beim Anfahren verhindern. Beispielsweise ist sie bei schlechtem Schienenzustand niedriger. Deswegen kann sie in der Realität z.B. witterungsbedingt abweichen.
2. Die Zugkraftkennlinie ist beim Beschleunigungsrechner nur in Form eines diskontinuierlichen Datensatzes und nicht in Form einer kontinuierlichen Kennlinie hinterlegt. Dabei kann es geringe Abweichungen durch die Berechnung geben.
3. Die Maximalgeschwindigkeit ist fahrzeugtechnisch reguliert. Z.B. durch Ungenauigkeiten in der Odometrie oder durch ein Gefälle können Geschwindigkeiten darüberhinaus erreicht werden.
4. Bei der Widerstandskennlinie kann es viele Abweichungen geben. Ein einfaches Beispiel hierzu ist der Luftwiderstand, der je nach Wetterlage anders sein kann. Hier sind ebenso idealisierte Kennlinienwerte unterstellt, die einen Standard repräsentieren. Aus der Widerstandskennlinie und der Zugkraftkennlinie kann dann auf die geschwindigkeitsabhängige Beschleunigungskennlinie geschlossen werden, die alle genannten Abweichungsmöglichkeiten in sich bergen.
5. Beim Fahrspiel selbst kann es weitere Abweichungen geben. Beim Rechner ist angenommen, dass das Beschleunigungsvermögen zur Gänze oder zu einem bestimmten Anteil ausgeschöpft wird. Über die Steuerung durch den Ausreizungsgrad des Beschleunigungsvermögens (Nr.5) kann es vorkommen, dass man den wahren Wert nicht wirklich trifft. Ohne den Ausreizungsgrad noch viel weniger.
Formeln und Herleitung der geschwindigkeitsabhängigen Beschleunigung
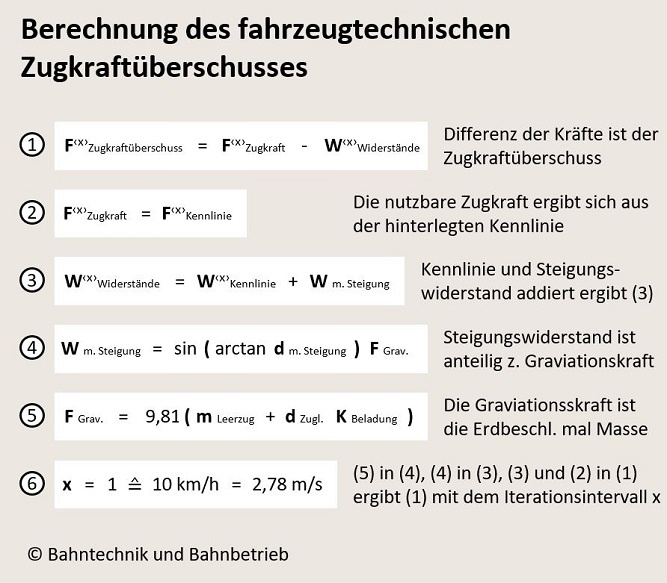
Alle Zwischenergebnisse miteinanderer verknüpft und in (1) eingesetzt, ergibt eine Kennlinie, welche den Zugkraftüberschuss beschreibt.
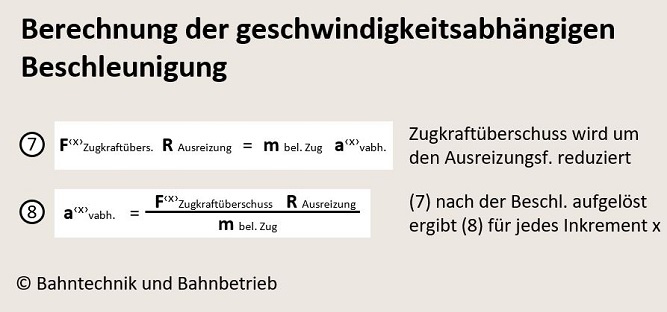
Aus der Kennlinie (1) lässt sich die Beschleunigung, ebenso als Kennlinie in dem besagten Intervall errechnen. Dabei wird der Zugkraftüberschuss um einen Ausreizungsfaktor gemindert, sodass nur der vom Fahrpersonal genutzte und abgerufene Kraftwert in die Rechnung mit eingeht (7).
Die entsprechende newtonsche Grundformel nach der Beschleunigung aufgelöst, ergibt dann (8).
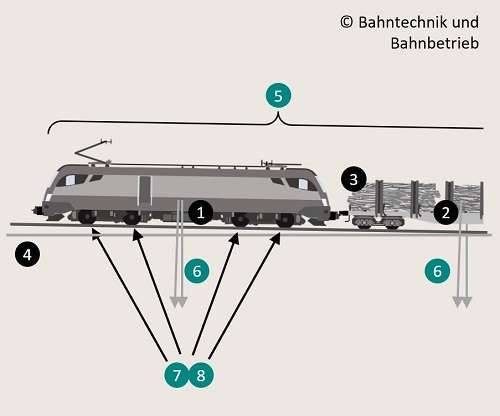
Um alle Formeln zum Beschleunigungsweg und zur Beschleunigungszeit sauber herleiten zu können, muss man sich an den vorherrschenden physikalischen Kräften einer Zugbeschleunigung orientieren: Der sogenannte Zugkraftüberschuss ist die übrig bleibende Restkraft, die sich aus den Motorenkräften des Zuges und den entgegenwirkenden Widerständen am Zug ergeben (1).
Die Motorenkräfte selbst sind beim Beschleunigungsrechner für jede Zugtype separat hinterlegt, und zwar als Zugkraft – Geschwindigkeitskennlinie (2). Die Kennlinie selbst ist in Geschwindigkeitsintervalle unterteilt, welche die Intervallbreite von 2,78 m/s haben (6). Das entspricht 10 km/h.
Ebenso sind die Widerstandskräfte hinterlegt. Sie beinhalten die in der Bahntechnik üblichen Kräfte wie Walkwiderstand, Reibungswiderstand, Luftwiderstand und die Widerstände durch rotierende Massen. Nicht enthalten ist der Steigungswiderstand, der separat in der Berechnungsmechanik des Beschleunigungsrechners berücksichtigt ist (3).
Der Steigungswiderstand beträgt den Sinuswert vom Steigungswinkel multipliziert mit der Gravitationskraft. Erstere wiederum kann über den Arcustangens aus der Tangentensteigung, angegeben in Promille, errechnet werden (4). Letztere berechnet sich durch die Erdbeschleunigung multipliziert mit der Gesamtmasse des Zuges (5).
Formeln und Herleitung der Beschleunigungszeit und des Beschleunigungsweges
Die Berechnung des Beschleunigungsweges geht aus der Berechnung der Beschleunigungskennlinie in (8) hervor. Doch bevor auf diese zuvor ermittelte Kennlinie zugegriffen wird, müssen eine neue, andere Iteration durchgeführt werden und hergeleitet werden: Es ist die Iteration nach der Zeit mit dem Intervall 1, welche für eine Sekunde steht (10). Innerhalb eines Iterationsschrittes ist die Beschleunigung konstant. Die Formel (9) enthält also kein t innerhalb eines solchen Iterationsschrittes.
Diese konstante Beschleunigung nach der Zeit integriert ergibt die Geschwindigkeit und somit die Formel (11). Diese abermals integriert nach der Zeit ergibt dann die allgemeine Beschleunigungswegformel (12).
Dann gelten die entsprechenden Anfangsbedingungen: Weg und Geschwindigkeit sind jeweils 0 (13). Die Anfangsbeschleunigung (14) entspricht dem ersten Iterationswert der Beschleunigungskennlinie aus (8).
(10) in (11) vereinfacht die iterative Berechnung (15). In dieser Iteration gilt als unbekannter Wert der zeitabhängige Beschleunigungswert. Dieser Wert ist übver die geschwindigkeitsabhängige Beschleunigungskennlinie abzulesen. Deswegen wird die zeitabhängige Geschwindigkeit mit der Geschwindigkeitsiteration aus (8) verglichen, und dann der entsprechend richtige Beschleunigungswert (16) in die zeitabhängige Formel von (15) gesetzt.
Das Analoge gilt für die Formel in (12), sodass daraus (17) folgt. Damit sind der Beschleunigungsweg berechnet, sobald die Iteration den entsprechenden Geschwindigkeitswert erreicht. Der Ergebniswert aus (15) steuert sozusagen die Iteration.
Die Beschleunigungszeit selbst ist dann mit dem Ende der Iteration am entsprechenden Iterationsschritt abzulesen (19).





































Dein Kommentar
An Diskussion beteiligen?Hinterlasse uns Deinen Kommentar!